Main Loops, Refresh Rates, and Determinism

On monitor refresh rate variability, how it interacts with deterministic results in a game, application, or simulation, and designing to fit this reality.

One of the first lessons in game, simulation, and application programming is on the “main loop”:

for(B32 should_quit = 0; should_quit == 0;)
{
  GatherInputs();  // get data encoding input from user
  Update();        // simulate, using new inputs
  Draw();          // draw state of simulation on screen
}

As simple as it looks, when you’re a brand new programmer, the above structure is not obvious.

It might seem ridiculous to experienced programmers to suggest that the above is not obvious to beginners! But a beginner doesn’t know the full space of possibilities. They’re constructing a picture of programming from a dozen loosely-correlated fragments—from dozens of unrelated tutorials, YouTube videos, and conversations. So, the “main loop” is an important lesson. It removes an important mental blocker in its answer to an important question—“how is a game structured?”

I heard a friend of mine once say that effective education involves “convenient lies”. A teacher can’t transmit his entire mental model to a student in a moment, so he needs to begin somewhere. So, to start, the teacher might tell the student something—a “convenient lie”—maybe with a brief caveat: “This isn’t the full picture, but assume that this is the case, and we’ll revisit this later.”

The “main loop” is one of these “convenient lies”, because as it turns out, it’s not the full story.

---

What It Means To “Draw”

First, note that a “main loop” is the programmatic implementation of a codecycle (in the terminology I introduced in my last post). After it completes its work for one iteration, it repeats. It is guaranteed to repeat under normal conditions, until state changes such that the “computational shape” of the system changes.

Furthermore, a “main loop” can be thought of as repeatedly accomplishing at least two tasks: (a) whatever is needed to simulate a game or execute an application’s logic for one “step”, and (b) telling the user about what happened during that “step”. The latter task includes “drawing”—or, in other words, changing pixel color values such that some visual output is communicated to the user via their monitor.

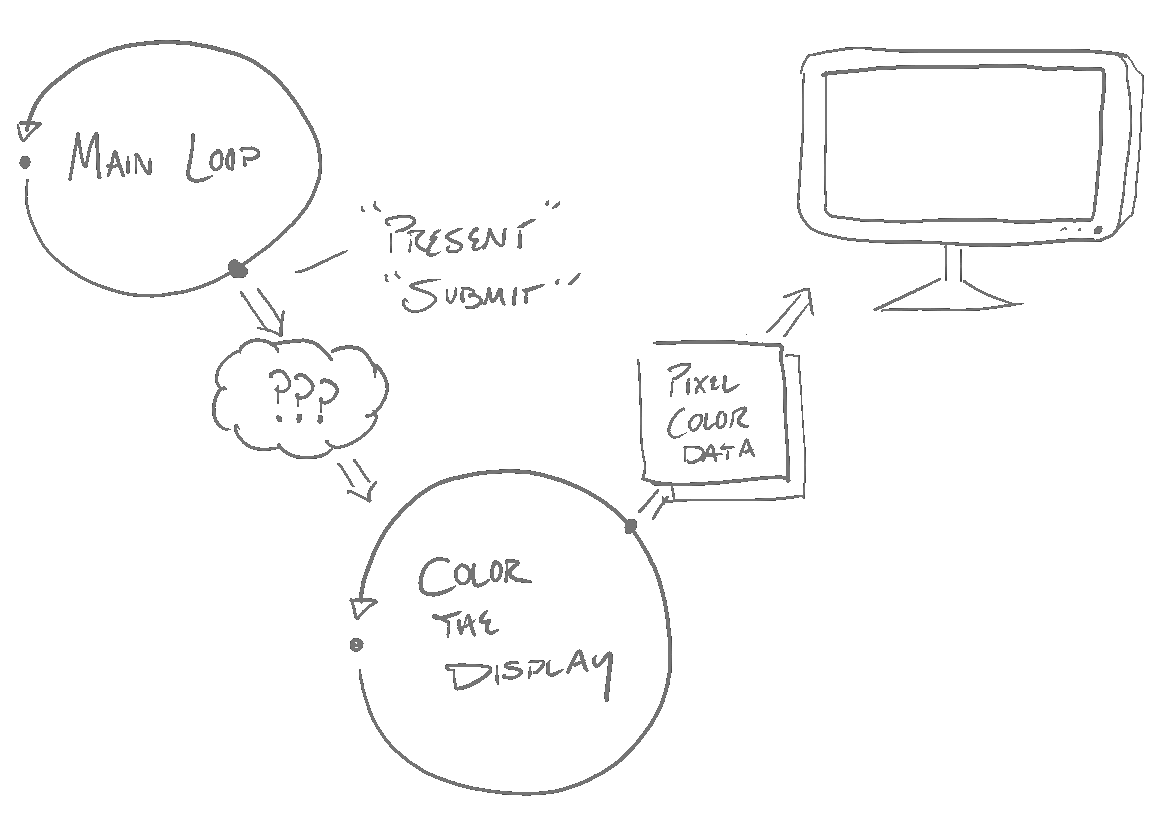
But dig into any game’s source code, and you’ll find that there’s not much in there about “changing pixel color values”. In fact, at the end of all of the “drawing” work—which seems to operate on a “frame buffer”—you’ll find something called “submit”, or “flush”, or “present”. Huh?

Submit to whom? Flush what? Present…? Who is changing the colors of pixels on the monitor?!

These days, a game or application exists within the context of an operating system, and draws to one (amongst many) windows, and executes in one (amongst many) processes. The entire system is not set up such that I can change arbitrary color values of arbitrary pixels—that might be pretty bad, actually, on a multitasking operating system! Furthermore, as soon as code which talks about pixel colors executes, the related monitor pixels do not literally change.

So what’s going on here? Let’s take a step back and look at the monitor’s end of the whole picture—we know the following:

• There are per-pixel values, somewhere, and they are directly used to determine how bright the tiny colored lights on a monitor are.

• Somewhere, someone changes those values, given new data about what those pixel color values should be.

• This needs to happen repeatedly, because new color data is repeatedly produced as applications are interacted with.

We also know the programmatic shape of something which happens repeatedly: a “main loop”. In other words, somewhere, someone is doing the high-level-equivalent of this (although surely it doesn’t look exactly like this):

for(;;)
{
  U32 *source_pixels = ...;       // from software
  U32 *destination_pixels = ...;  // to monitor
  for(int pixel_index = 0; pixel_index < num_pixels; pixel_index += 1)
  {
    destination_pixels[pixel_index] = source_pixels[pixel_index];
  }
}

And finally, we know that the above is an implementation of a codecycle. So when a main loop “presents”, or “flushes”, or “submits”, it’s transmitting some information to another codecycle, which will eventually lead to a transmission of pixel data to the codecycle which is coloring the display’s pixels. Now, the picture of how a “main loop” relates to the display has become clearer:

The space in between these two codecycles is, by itself, a rich and complex pipeline. If the application’s main loop is executing within a multitasking operating system environment, then there is an entire “compositor” system, which has the task of composing display data from multiple applications. Even at the high level, there are numerous twists and turns in how this entire story comes together—the implementation details surely introduce many more. That in itself is an interesting topic, the details of which are well beyond my knowledge and skillset, and also well beyond the scope of this post, so I’ll move on.

---

Codecycle Cycles Per Second

Two codecycles in a single system execute independently from each other, but nevertheless they must communicate. How exactly that works depends on the desired characteristics of the system in question.

First, let’s note the obvious fact that computation is not free—there is a time cost associated with every instruction which executes in any codepath. There is therefore a time cost associated with every cycle of a codecycle, which is the sum of the time cost associated with every instruction in one cycle. This can be measured as it’s measured everywhere else—cycles-per-second (Hz).

In some cases, it is desirable to enforce that each cycle is uniform in its time cost. In other cases, a codecycle may be designed to execute as rapidly as possible given a variety of workloads.

In the case of monitors, it’s usually the former. A monitor is normally designed to repeatedly adjust the color values which are used to light its pixel lights (“refresh”) at a fixed rate. This is the monitor’s “refresh rate”, and it varies quite a bit.

The most common case for consumer device monitor refresh rate is—by far—60 Hz, meaning the monitor will refresh 60 times per second. But this is by no means a guarantee—sizable numbers of consumer devices update at 120 Hz, or 144 Hz, or sometimes even 240 Hz (and sometimes even higher, despite the fact that almost every interesting game and many interesting applications do not operate that quickly—and thus will miss many of their frames on such monitors).

In the case of a game’s “main loop”, it’s also usually the former. A game is designed to run at some fixed simulation rate—usually it’s 30 Hz or 60 Hz. In older games—like The Legend of Zelda: Ocarina of Time—it’s common to find even lower, like 20 Hz.

Historically, the choice of 20, 30, or 60 Hz were preferable in that they matched or cleanly divided into a monitor’s refresh rate. If a monitor refreshes 60 times per second, and a game refreshes 60 times per second, no problem—every time the monitor refreshes and presents a new frame, the game will have provided one. Given the same monitor, but a game which refreshes 20 or 30 times per second, also no problem—the monitor will just have a new frame every 2 or 3 cycles. It’ll feel a bit choppier, but it’ll still look and feel like a smooth simulation.

You might notice that there’s a little problem, though—a 20, 30, or 60 Hz game with a 60 Hz monitor makes sense—but what exactly happens to a 20, 30, or 60 Hz game with a 144 Hz monitor? That doesn’t cleanly divide at all. And this is an actually common case in the modern world—quite important to get right. So what happens?

At this point, there are two choices for a “main loop”.

First, a game may simply use the same approach which was used for, for instance, a 30 Hz simulation loop with a 60 Hz monitor, just without the baked in assumption that they have two refreshes per simulation. Sometimes, a 144 Hz monitor presenting a 30 Hz game will just have the same frame for 4 cycles, and sometimes it’ll be for 5 cycles—it might stutter a bit, it might feel a bit less smooth, it’ll feel just as slow as 30 Hz, but things still somewhat work.

F32 monitor_dt = ...;   // grab from monitor
F32 sim_dt = 1.f/60.f;  // fixed for this simulation
F32 last_sim_time = 0.f;
F32 sim_time = 0.f;
for(B32 should_quit = 0; should_quit == 0;)
{
  sim_time = GetCurrentSimTime();
  for(;sim_time >= last_sim_time + sim_dt;)
  {
    GatherInputs();
    Update(sim_dt);
    last_sim_time += sim_dt;
  }
  Draw();
}

Of course, this is a bit unfortunate. The game may look and feel a bit worse by stuttering—worse than it already would just by running much slower than the refresh rate. Someone purchasing a 144 Hz monitor does so for the smoothness—by just running at a fixed rate regardless of monitor, a game eliminates that benefit for them.

So, another option would be to always run at the refresh rate. A simulation step is always parameterized by whatever we’d like our timestep to be—1/144th of a second on a 144 Hz monitor, and 1/60th of a second on a 60 Hz monitor—and we’re done.

F32 monitor_dt = ...; // grab from monitor
F32 sim_dt = monitor_dt;
for(B32 should_quit = 0; should_quit == 0;)
{
  GatherInputs();
  Update(sim_dt);
  Draw();
}

…Sounds great, but as it turns out, it’s not that simple.

---

Determinism

The primary problem with adopting the responsibility of simulating at possibly-many timesteps is with a simulation’s determinism. In other words, do the contents of state_c and state_b match those of state_a once the following code has executed?

State *state_a = StateAlloc();
State *state_b = StateAlloc();
State *state_c = StateAlloc();

Update(state_a, 1.f/30.f);

Update(state_b, 1.f/60.f);
Update(state_b, 1.f/60.f);

Update(state_c, 1.f/120.f);
Update(state_c, 1.f/120.f);
Update(state_c, 1.f/120.f);
Update(state_c, 1.f/120.f);

Now, if you took the above code and filled out a definition of State, StateAlloc, and Update, we could answer that question—and the answer would depend on that with which we filled those definitions. For instance, here is an implementation for which the answer would definitely be “yes”:

struct State
{
  int x;
};

State *StateAlloc(void)
{
  State *state = malloc(sizeof(State));
  state->x = 123;
  return state;
}

void Update(State *state, F32 dt)
{
  // do nothing
}

On the other hand, here is an implementation for which the answer would be “no”:

struct State
{
  int x;
};

State *StateAlloc(void)
{
  State *state = malloc(sizeof(State));
  state->x = 0;
  return state;
}

void Update(State *state, F32 dt)
{
  state->x += 1;
}

But here is a similar implementation for which the answer would be “yes” (at least, if you ignore differences in floating point error):

struct State
{
  F32 x;
};

State *StateAlloc(void)
{
  State *state = malloc(sizeof(State));
  state->x = 0.f;
  return state;
}

void Update(State *state, F32 dt)
{
  state->x += dt;
}

If we replaced the above definitions with those for an actual game or simulation, the answer is still “it depends”. A codepath falls into one category or another. But generally, for a large number of popular techniques for animation, physics, and gameplay programming, they are generally not deterministic with respect to timestep (sometimes by design). In other words, results may dramatically vary depending on timestep.

Now, in some cases, small differences are acceptable. One example of this is with user interface animation, which I’ve briefly mentioned before. In this case, animations are about extra communication to a user—they do not (and ought not to) have direct implications on the logical functioning of the program. Animation code can be written to be robust to multiple timesteps, such that animations complete in the same amount of wall-clock time (with nearly identically appearing characteristics) irrespective of refresh rate. Small floating point results will not be deterministic in general, but it is simply irrelevant in this case.

For instance, when it comes to common user interface animations, I prefer this, given its simplicity, its behavioral characteristics as target changes, and its overall applicability to a user interface’s design:

current += (target - current) * rate;

You may be wondering: Is the above deterministic with respect to refresh rate (given that current and target are independent of refresh rate)? The answer is: It depends on rate. If rate is a constant—like 0.5—then no. The answer is still no even if the rate is a constant multiplied to dt.

But, a rate can be calculated such that it is independent of refresh rate (floating point error notwithstanding), by appropriately considering how dt is being multiplied and where across many frames:

F32 rate = 1 - Pow(2, (-50.f * dt));

Nevertheless, there is a large category of simulation techniques which are unacceptably nondeterministic with respect to timestep. The downstream effects of this could mean that a game written with such techniques simply feels differently across different monitors. It could also mean that the game is unplayable on different monitors—a jump in a platformer could simply be possible with one timestep, and impossible with another. Collision detection could work well with one refresh rate, and players could fall through the floor on another.

So, options for a “main loop” are further limited. Unless the main loop can be written such that it’s effectively timestep independent (which, if you ask game programmers about this, many of them will just laugh), and unless you’re fine with possibly-drastic nondeterministic effects, then the only solution is to fix the simulation timestep in place—or, at the very least, constrain it to a well-defined range.

Let’s say, then, that we’ve decided on a fixed timestep—it eliminates a whole bunch of seemingly needless problems. Can our “main loop” change at all to still support the benefits of a higher refresh rate, and avoid the drawbacks of jitter?

---

Interpolation

As it turns out, yes. There is a well-known article on this topic by Glenn Fiedler in which he discusses exactly this topic. Fielder begins with one approach I mentioned earlier—the main loop is adjusted such that it cycles at the monitor’s refresh rate, but simulation occurs at a fixed rate:

F32 monitor_dt = ...;   // grab from monitor
F32 sim_dt = 1.f/60.f;  // fixed for this simulation
F32 last_sim_time = 0.f;
F32 sim_time = 0.f;
for(B32 should_quit = 0; should_quit == 0;)
{
  sim_time = GetCurrentSimTime();
  for(;sim_time >= last_sim_time + sim_dt;)
  {
    GatherInputs();
    Update(sim_dt);
    last_sim_time += sim_dt;
  }
  Draw();
}

But instead of Draw merely using the current state, it uses both the current and the previous:

F32 monitor_dt = ...;   // grab from monitor
F32 sim_dt = 1.f/60.f; // fixed for this simulation
F32 last_sim_time = 0.f;
F32 sim_time = 0.f;
State *current_state = ...;
State *last_state = ...;
for(B32 should_quit = 0; should_quit == 0;)
{
  sim_time = GetCurrentSimTime();
  for(;sim_time >= last_sim_time + sim_dt;)
  {
    GatherInputs();
    Update(current_state, sim_dt);
    last_sim_time += sim_dt;
    last_state = StateCopy(current_state);
  }
  Draw(last_state, current_state);
}

In this setup, the simulation occurs at a fixed timestep, and drawing occurs at the monitor’s refresh rate. When drawing occurs, it uses the current time to sample between the current and previous states, when possible. If an object moved from point A on step 0, then to point B on step 1, and Draw occurs such that it’s halfway inbetween step 0 and 1, then the object will be drawn at point (A+B)/2.

This would be implemented using techniques like linear interpolation (in the case of positions). This is certainly good enough to produce good results given common game simulation and drawing rates. That being said, if it ever was not good enough (which, frankly, I find doubtful for all common cases), then the quality of interpolation may be further improved with more sophisticated interpolation functions. For instance, instead of using two recent states, Draw may use three, and interpolate some properties with a function with a more sophisticated shape.

This approach indeed works, but there are some caveats, and you might notice some issues or have some concerns.

Discrete States

Interpolation seems like it’d work well with many pieces of information in a simulation. Two world-space positions, two velocities, and two colors may be linearly sampled. Two quaternions encoding an object’s rotation may be slerp’d or nlerp’d between.

But what about information which is not assumed to merely be samples from a continuous function? That is, information which is sampled from functions with discontinuities?

For one example, imagine an object teleporting in a game. Is it correct to interpolate between that object’s original position and its destination position? Probably not—there is some point in time at which the object had not yet teleported, and there was some discrete moment at which the object had teleported.

Similarly, imagine an object not existing on simulation step n, but beginning to exist at simulation step n+1. If a frame is being produced by sampling from both of these states, what happens?

The short answer is, there is no one-size-fits-all answer—but reasonable decisions can be made given extra context.

In the case of an object teleporting, generational indices may be used, such that position interpolation only occurs if the position generational index at step n is the same as that at step n-1. When a teleportation occurs, that generational index is incremented. The two discontinuous steps will thus disagree on the generational index, and no interpolation will occur.

The same approach can be used in case of an object’s identity changing between two steps—for instance, if it does not exist on one step and does on the next. Or, if an object at some slot is literally a different object, as that slot had been freed and reallocated for some other purpose. Generational indices may be used to signify new generations with respect to certain properties.

Furthermore, disagreeing generational indices do not necessarily imply that all interpolation is lost in all cases. If an object’s position generational index changes, then one possibility is drawing the object twice—once at its original position, once at its destination position—with a transparency value at each position determined by the sampling time. In that case, the object will fade from one position to another.

But, setting those techniques aside, the simplest approach given such discrete, non-continuous states is to default to using just one of the states.

In my view, either option is perfectly acceptable for discrete, discontinuous states. At the end of the day, behavior appearing smoothly on a higher refresh rate monitor is by nature about continuous functions. For logical, discrete changes, increasing refresh rate does not logically change the meaning nor feeling of a visualization of such changes.

There are some tradeoffs in deciding between the most recent state and the second-most recent state. If the newest state is chosen, the exact visual timing will indeed differ between two refresh rates—the most recent state will be visible more quickly on a 144 Hz monitor than it will be on a 60 Hz monitor. This may be preferable in that it minimizes display latency of new information when possible. If the older state is chosen, then the latency will not as meaningfully differ between two refresh rates, but instead will be higher in all cases.

In some cases, these tradeoffs may matter—I do not want to assume they don’t, and so I’d rather mention them rather than ignore them—but I haven’t thought of a case in which they do. Personally, I would opt for choosing the most recent state as a default, given that it minimizes latency where possible, and the differences in latency between refresh rates will probably not be meaningful, given their size as compared to a human’s reaction time to discrete, logical, discontinuous information.

Extra Latency

In the above sample code, Draw necessarily occurs after the most recent state is produced, yet it is sampling between the most recent state and the state before that. This requires that—for a change in simulation state to be used by Draw—at least the timespan of one simulation step must pass. If a simulation step is 30 Hz, then at least 33ms will pass before Draw will be able to use that step’s information.

This ultimately results from the decision to use only multiple states produced by the simulation. The latency incurred is ultimately small in comparison to other sources of latency in the whole pipeline from user, to simulation, and back to user, but it seems relatively unavoidable given this approach.

There are, however, useful techniques in minimizing the impact of this latency. One—used in virtual reality, called “late latching”—exploits the fact that camera position and orientation can be updated much later in a drawing pass than the bulk of simulation state. By the time drawing actually occurs, the camera position and orientation may be updated in accordance with newer inputs than those used for the purposes of older simulation steps.

Late latching may be further combined with depth-based reprojection—also a technique historically coupled with virtual reality—in order to update camera eye and orientation well after it has been used to draw.

In my view, these techniques make the worst of the latency problems incurred by this structure—if they were not already too small to care for—solvable. Latency matters in that it separates cause and effect of a user’s input and its impact on a simulation. The tightest cause and effect loop for players of games, or users of simulations—and by far the one with most noticeable latency—is mouse movement, and what it controls in a simulation. This is precisely the cause and effect loop for which late latching and depth-based reprojection are intended. Other latency is—generally—less relevant.

State Duplication Cost

You might have one potential concern of the above sample code in the following line:

last_state = StateCopy(current_state);

How expensive would that realistically get? How much extra cost does it incur, as opposed to only storing and mutating a single state? Is it a meaningful cost? Is it worth it for doing this interpolation work?

As usual, the answer is that “it depends”, given that it’s such an abstract snippet of code.

But, some conservative, back-of-the-napkin math will provide some insight.

It is hard to be precise given the variability in possible hardware, but a fair assumption for memcpy bandwidth on a common consumer Intel x64 CPU would be something like 5-10 GB/s. Let’s assume StateCopy is more-or-less a memcpy (because we’ve responsibly designed it as such, rather than being a forest of pointers to individually-heap-allocated objects), at 5 GB/s bandwidth. If the simulation occurs 60 times per second, that suggests StateCopy has a bandwidth of 83 MB/step.

But, of course, we also have real simulation work to do—we can’t simply copy the state repeatedly without doing nothing. So let’s assume further that it can only copy ~10% of that (with the remaining 90% being used for simulation) at 8.3 MB/step.

This means that we can copy 8.3 MB per 60 Hz simulation step. If the state for each object in our simulation weighs about 0.5 KB, then we can copy ~16,000 of them per 60 Hz simulation step.

Now, that’s not infinity objects! But… it’s quite a lot—in fact, more than most games and simulations need.

But what if we need more? Are we just out of luck? No. These are the numbers for the most naïve duplication, via a direct memory copy. We’ve assumed all data for all objects is relevant for drawing. We’ve also assumed that all objects constantly update (rather than a small non-static set of them)—which is likely not the case. Furthermore, an even tighter copy can avoid copying state at all, and merely copy and apply state deltas.

As usual, the exact endgame here strongly depends on the circumstances. But it’s enough, for me, to conclude that a first pass solution with the naïve memcpy can bear quite a lot of weight. Thus, I think it is sufficient in usual cases.

Heterogeneous Iterations

That brings me to perhaps the most subtle issue of the above main loop structure—one which is not so easily addressed.

This structure has introduced many kinds of main loop iterations. It has not simply bifurcated the possible computational shape of one loop iteration—it has introduced several, depending on how many simulation steps may occur in one iteration. Either one iteration performs n simulation steps then draws, or, it only draws. These many codepath versions are distinct. The main loop repeatedly switches between these shapes as needed.

If care is not taken, this may impact the correctness and determinism of some behaviors. For instance—will code behave identically if two simulation steps happen on a given iteration as opposed to one? As opposed to zero? What if some side effects are caused by a non-simulating iteration (perhaps side effects related to input)—does that behave identically as the same side effects being caused on a simulating iteration?

Another frustrating aspect of this is that it impacts debuggability and profiling. “Capturing a frame”, or “stepping through a frame”, can now mean one of many things.

Because “one frame” can mean one of many things, the performance of “one frame” can mean one of many things. One particular scene may draw in a reasonable amount of time, but when putting it next to one, two, or three simulation steps, it causes unpleasant hitches and performance issues. This fact also makes it much more difficult to make assumptions about time budgets, and how much work we can expect our game or simulation to actually accomplish.

In short, this issue can be summarized in the following way. All code which runs in one main loop iteration now executes in many contexts, and whether or not that code is “correct” (performs the logically correct behavior, performs at the required—or better—performance target) is now dependent on a new variable. Because this variable is introduced at the topmost level of our program, it impacts all code eventually called by that topmost level.

Must we simply accept these drawbacks, then, for all code ever? Or is there a way to eliminate this extra variability we’ve introduced into the core structure of our program?

---

Ditching The Main Loop

The above main loop structure tries to balance the constraints of deterministic simulation, variable refresh rates, and drawing with interpolated state. Because this codepath is pressured from so many angles, it is forced to contort and bend. This is the ultimate cause of the extra complexity which the original, simple, flat main loop structure lacked.

When considering this problem, I had a hunch that the main loop was now doing too much, and a simpler solution—which avoids the issues described in the previous section—might emerge from a different top-level structure.

In the same way that arenas are a useful construct to bundle lifetimes within a single codecycle, I thought that codecycles can be considered as a useful construct to bundle timelines. We want a game simulation step to run at a fixed rate—let’s say 60 Hz. We also want a drawing step to run at a fixed rate—whatever the refresh rate of the monitor is. These timelines fundamentally do not agree. Our attempt to merge them led to some ugly consequences. So, perhaps they ought to be different.

Instead of dying on the hill of a single top-level, single-threaded main loop, we can have multiple codecycles—multiple little computational “engines”—running independently. One for game simulation, one for drawing.

This design leads to some interesting consequences.

First, notice that the issue of heterogeneous iterations is gone. The simulation codecycle repeatedly performs the same tasks without any bifurcation of the top-level structure of the iteration. After every simulation timestep, it submits its state to be used by the drawing codecycle. Similarly, the drawing codecycle also has a uniform top-level structure. It pulls new simulation states when possible, and draws, still interpolating between the two most recent simulation states. This separation allows simulation to not be in lockstep with drawing, and vice versa. The simulation does not need to “make room” for drawing—it has much closer to the full timestep to do useful work.

Second, notice that because simulation and drawing are separate and operate entirely independently, the simulation’s continued operation is not coupled to the overall program’s ability to provide live, useful feedback, like a live, interactable user interface providing real-time information about the simulation. If the simulation is manually paused, if it hangs, or if its associated thread is frozen, the rest of the system may continue operating like normal.

Third, this design has put us in a great position for other benefits. This design has pressured us to organize state such that it’s easily deep-copied, easily used to parameterize a drawing pass, and easily transferred. Furthermore, it has pressured our simulation to be written such that it operates independently from our drawing. Thus, any debugging or design tools which use simulation state recording, replaying, or timeline scrubbing—much like those demonstrated in the Tomorrow Corporation Tech Demo—are now much more within our reach.

---

Closing Thoughts

I wrote this post after trying exactly what I described. I’ve been quite happy with the results. Writing both simulation and drawing code is nearly as simple as within a non-interpolated single-threaded context, and the basic machinery for communicating between the multiple top-level codecycles is simple enough.

In the project I’m working on, I simulate at a fixed 30 Hz on an isolated game thread, and I do both drawing and user interface work on a “user thread”, which cycles at the monitor refresh rate. Given this top-level structure, it’s also trivial to separate input gathering—which includes details like window moving and resizing—to another thread, which allows simulation and drawing to operate smoothly even as a window is moved or resized. I did that in my project as well, and pulled input gathering into its own “input thread”.

At the end of the day, the entry point of the program’s main thread becomes tasked only with setting up shared data structures (used for communication between the various top-level threads), and launching them:

In my view, this close reexamination of the main loop has led me to a top-level architecture with a number of worthwhile benefits. I hope this post helped lead you to those same benefits, demystify this problem, or was at least interesting.

---

If you enjoyed this post, please consider subscribing. Thanks for reading.

-Ryan